[Javascript로 정리하는 이코테] 6. 이진 탐색

http://www.yes24.com/Product/Goods/91433923

이것이 취업을 위한 코딩 테스트다 with 파이썬 - YES24

 

개념

• 이진 탐색을 이용하면 배열 내에서 데이터를 매우 빠르게 탐색할 수 있다.
• 이진 탐색을 이해하기 위해서는 우선 순차 탐색에 대해 알아야 한다.

 

순차 탐색

• 배열 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법이다.
• 주로 정렬되지 않은 배열에서 데이터를 찾아야 할 때 사용한다.
• 시간복잡도: O(n)

 

예제 7-1. 순차 탐색

const sequentialSearch = (n, target, arr) => {
  for (let i = 0; i < n; i++) {
    if (target === arr[i]) return i + 1;
  }
};

const n = 5;
const target = 'Dongbin';
const arr = ['Haneul', 'Jonggu', 'Dongbin', 'Taeil', 'Sangwook'];

console.log(sequentialSearch(n, target, arr));

 

이진 탐색

• 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다.
• 탐색 범위의 시작점, 끝점, 중간점을 가지고, 찾으려는 데이터와 중간점 위치의 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 방법이다.
• 이진 탐색을 사용하기 위해서는 배열 내부 데이터가 반드시 정렬되어 있어야 한다.
• 시간복잡도: O(logn)

 

예제 7-2. 재귀 함수로 구현한 이진 탐색

const binarySearch = (arr, target, start, end) => {
  if (start > end) return -1; //원소가 존재하지 않는 경우

  const mid = ~~((start + end) / 2);
  if (target === arr[mid]) return mid;
  else if (target < arr[mid]) return binarySearch(arr, target, start, mid - 1);
  else return binarySearch(arr, target, mid + 1, end);
};

const n = 10;
const target = 7;
const arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];

const start = 0, end = n - 1;
console.log(binarySearch(arr, target, start, end) + 1);

 

예제 7-3. 반복문으로 구현한 이진 탐색

const binarySearch = (arr, target, start, end) => {
  while (start <= end) {
    const mid = ~~((start + end) / 2);
    if (target === arr[mid]) return mid;
    else if (target < arr[mid]) end = mid - 1;
    else start = mid + 1;
  }

  return -1;
};

const n = 10;
const target = 7;
const arr = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];

const start = 0, end = n - 1;
console.log(binarySearch(arr, target, start, end) + 1);

 

💡 코딩 테스트에서의 이진 탐색

• 단골 문제이니 반드시 위 코드를 외우자!
• 처리해야 할 데이터의 개수가 1,000만 단위 이상으로 넘어가면, 이진 탐색과 같이 O(logn)의 속도를 내야 하는 알고리즘으로 문제를 풀어야 하는 경우가 많다.
• 데이터의 개수가 1,000만(10^7) 개를 넘어가거나, 탐색 범위의 크기가 1,000억(10^11) 이상이라면, 이진 탐색 알고리즘을 의심해 보자.

 

참고) 자바스크립트의 빠른 출력

일반적인 출력 방식인 console.log()를 사용하면 출력이 매우 많은 경우 시간 초과가 발생할 수 있다. 이때는 하나의 문자열을 통해 결과값을 더하고 마지막에 한 번만 출력해야 한다.

 

 

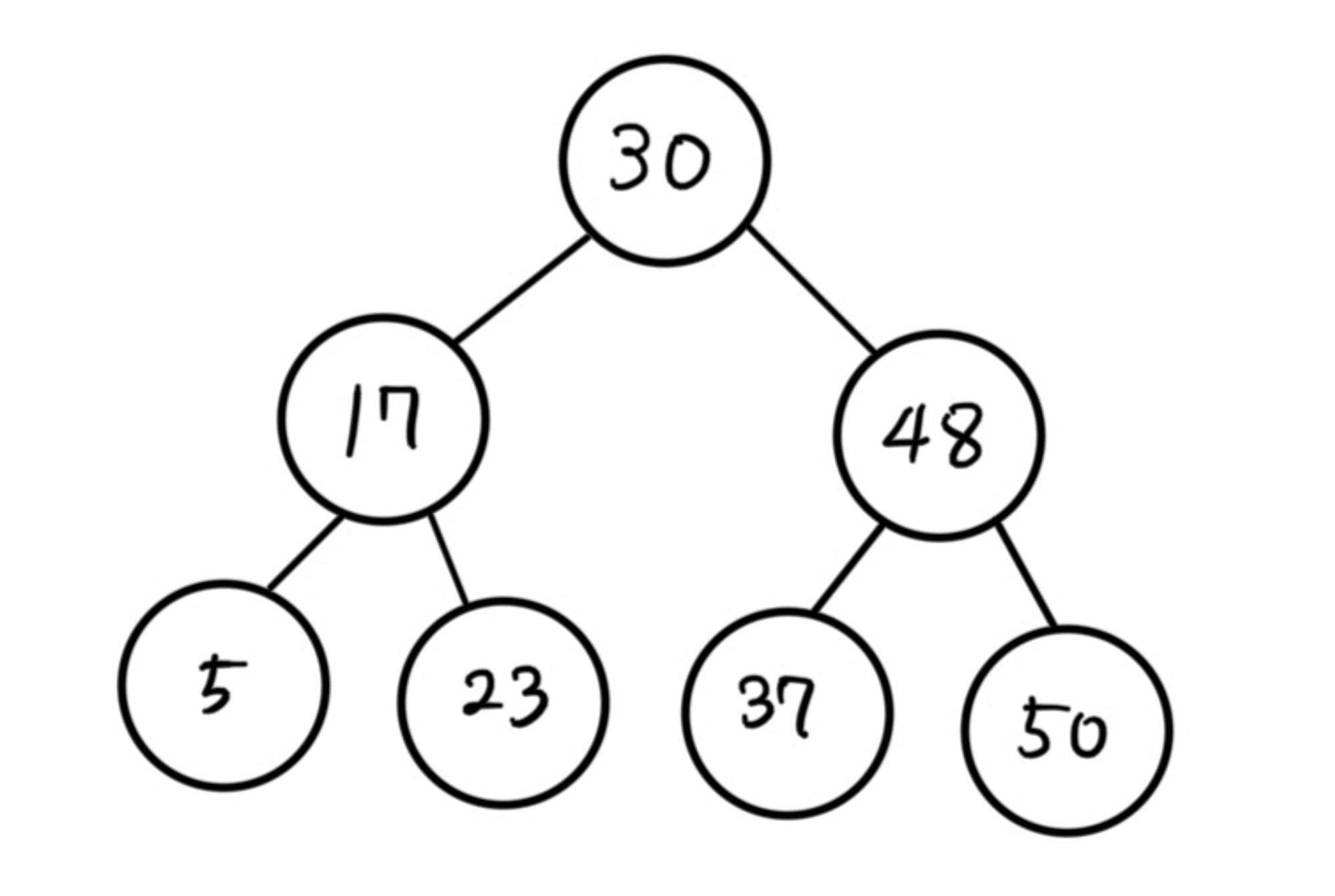
이진 탐색 트리

• 이진 탐색 트리는 이진 탐색이 동작할 수 있도록 고안된, 효율적인 탐색이 가능한 자료구조로 트리의 가장 간단한 형태이다.
• 이진 탐색 트리는 다음과 같은 특징을 가진다.
  • 왼쪽 자식 노드는 항상 부모 노드보다 작다.
  • 오른쪽 자식 노드는 항상 부모 노드보다 크다.

binary search 예시

 

 

실전 문제

부품 찾기

방법 1. 이진 탐색 → O((n+m) logn)

const fs = require('fs');
let input = fs.readFileSync('../tc.txt').toString().trim().split('\n');

let [n, arr, m, req] = input;
n = +n;
arr = arr.split(' ').map((v) => +v);
m = +m;
req = req.split(' ').map((v) => +v);

const binarySearch = (arr, target, start, end) => {
  const sorted = arr.sort((a, b) => a - b);

  if (start > end) return -1;

  const mid = ~~((start + end) / 2);
  if (target === sorted[mid]) return mid;
  else if (target < sorted[mid])
    return binarySearch(arr, target, start, mid - 1);
  else return binarySearch(arr, target, mid + 1, end);
};

function solution(n, m, arr, req) {
  let ans = '';
  for (const target of req) {
    if (binarySearch(arr, target, 0, n - 1) !== -1) ans += 'yes ';
    else ans += 'no ';
  }
  return ans;
}

console.log(solution(n, m, arr, req));

 

방법 2. 계수 정렬 → O(n+m)

function solution(n, m, arr, req) {
  let store = [...Array(Math.max(...arr) + 1).fill(false)];
  arr.forEach((v) => (store[v] = true));

  let ans = '';
  for (const target of req) {
    if (store[target]) ans += 'yes ';
    else ans += 'no ';
  }
  return ans;
}

 

방법 3. 집합 → O(n+m)

function solution(n, m, arr, req) {
  let store = new Set(arr);

  let ans = '';
  for (const target of req) {
    if (store.has(target)) ans += 'yes ';
    else ans += 'no ';
  }
  return ans;
}

console.log(solution(n, m, arr, req));

 

떡볶이 떡 만들기

• 전형적인 이진 탐색 문제이자, 최적화 문제를 결정 문제(yes/no로 답하는 문제)로 바꾸어 해결하는 파라메트릭 서치(parametric search) 유형이다.
• 원하는 조건을 만족하는 가장 알맞은 값을 찾는 문제에서 주로 파라메트릭 서치를 사용한다.
• 범위 내에서 조건을 만족하는 값을 찾을 때, 이진 탐색으로 결정 문제를 해결해 가며 탐색 범위를 좁혀갈 수 있다.
• 이러한 파라메트릭 서치 유형의 경우, 이진 탐색을 반복문으로 구현하는 것이 더 쉽고 간결하다.

const fs = require('fs');
let input = fs.readFileSync('./tc.txt').toString().trim().split('\n');

let [nm, arr] = input;
const [n, m] = nm.split(' ').map((v) => +v);
arr = arr.split(' ').map((v) => +v);

let ans = 0;
const binarySearch = (arr, target, start, end) => {
  while (start <= end) {
    const mid = ~~((start + end) / 2); //현재 h
    const sum = arr.map((v) => (v < mid ? 0 : v - mid)).reduce((a, b) => a + b);

    if (target <= sum) {
      //필요한 떡의 길이보다 큰 경우
      start = mid + 1;
      ans = mid;
    } else {
      //필요한 떡의 길이보다 작은 경우
      end = mid - 1;
    }
  }

  return ans;
};

function solution(n, m, arr) {
  return binarySearch(arr, m, 0, Math.max(...arr));
}

console.log(solution(n, m, arr));